Auf dieser Seite finden sie viele verschiedene Rätsel-Formen.
Die meisten Aufgaben sehen beim ersten Hinschauen sehr leicht aus, aber das täuscht. Einige Rätsel sind in der Tat rätselhaft und extrem schwierig. Andere wiederum sind relativ leicht – wenn man den nötigen Grips dazu hat.
Es gibt leichte Aufgaben und Rätsel, es gibt auch schwere Aufgaben, die eine gewisse Intelligenz vorausetzen und dann habe extrem schwere bzw. kniffelige Aufgaben und Rätsel , die, und das haben alle gemeinsam, alle lösbar sind.
Aufgabe 1
Ist doch kinderleicht ?
Sehen sie sich alle bunten Zahlen genau an! Haben sie nichts Auffälliges gefunden?
Gehen sie noch einmal alles ganz langsam in Ruhe durch! Betrachten sie bitte das ganze Bild ganz genau!
Hier geht es zur Lösung der Aufgabe 1
Aufgabe 2
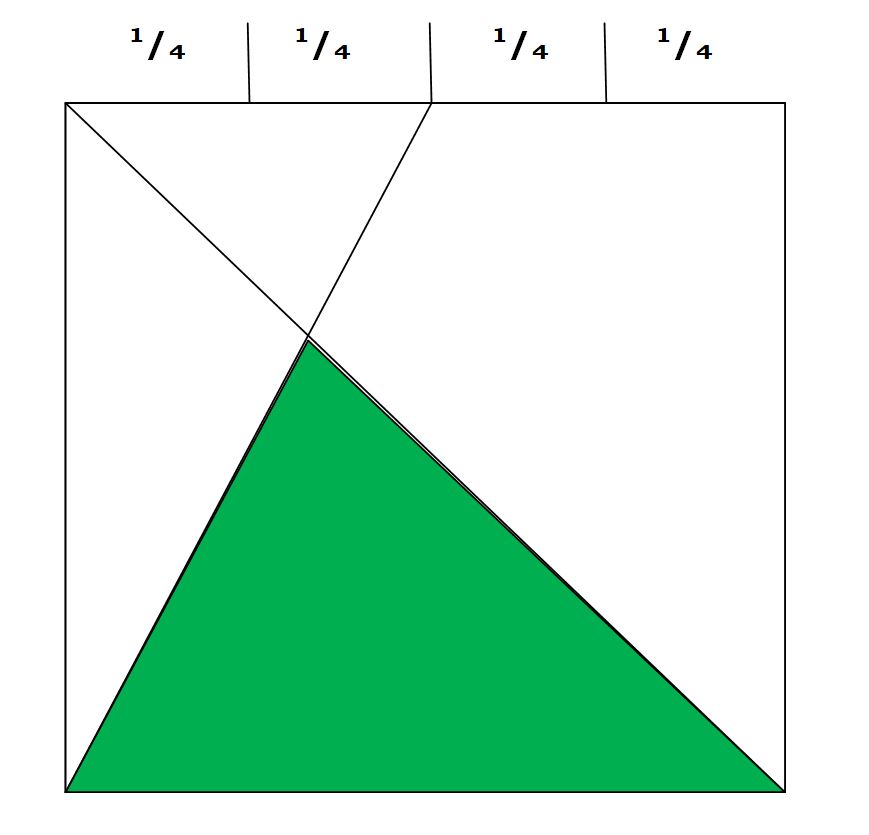
Die Frage lautet: Die Fläche des Vierecks ist gleich 100 cm². Wie groß ist die Fläche des grünen Dreiecks?
Oder anders gefragt: Wie groß ist der Anteil des grünen Dreiecks bezogen auf das Quadrat?
Eine kleine Hilfe gebe ich Ihnen.
Allgemein gilt: Die Fläche eines Dreiecks ist die halbe Grundseite mal die Höhe.
Ist also zum Beispiel die Grundseite des Dreiecks 10 cm lang und die Höhe des Dreiecks 8 cm, dann beträgt die Fläche des Dreiecks die halbe Grundseite, also 10:2 mal die Höhe 8, also 5 mal 8 gleich 40 cm². Da das Quadrat mit dem grünen Dreieck die Maße 10 mal 10 cm hat, wissen wir also jetzt, dass die Grundseite des grünen Dreiecks 10 cm beträgt.
Und noch etwas verrate ich Ihnen. Das kleine Dreieck am oberen Rand links ähnelt dem großen grünen Dreieck. Es steht quasi bezogen auf das grüne Dreieck auf dem Kopf und hat eine Grundseite, die genau die Hälfte des großen grünen Drteiecks beträgt. Für uns bedeutet dies, dass das kleine Dreieck eine kleinere Version des großen grünen Dreiecks ist.
In der Mathematik heißt es: Eine Eigenschaft von ähnlichen Dreiecken ist, dass das Verhältnis der Grundseiten zueinander dasselbe ist, wie das Verhältnis der Höhen. Da die Grundseite des grünen Dreiecks doppelt so groß ist wie die des kleinen Dreiecks, ist die Höhe des großen grünen Dreiecks ebenfalls doppelt so groß.
Und noch etwas verrate ich Ihnen: Wenn das Quadrat, in welchem sich die Dreiecke befinden, eine Kantenlänge von 10 cm hat, dann beträgt die Höhe des grünen Dreiecks plus der Höhe des kleinen sogenannten ähnlichen Dreiecks auch 10 cm.
Mehr verrate ich jetzt aber nicht.
Noch einmal: die Frage lautet: Wenn das Quadrat 100 cm² groß ist, wie groß ist dann die Fläche des grünen Dreiecks.
Hier geht es zur Lösung der Aufgabe 2
Aufgabe 3
Die Dreiecksfrage
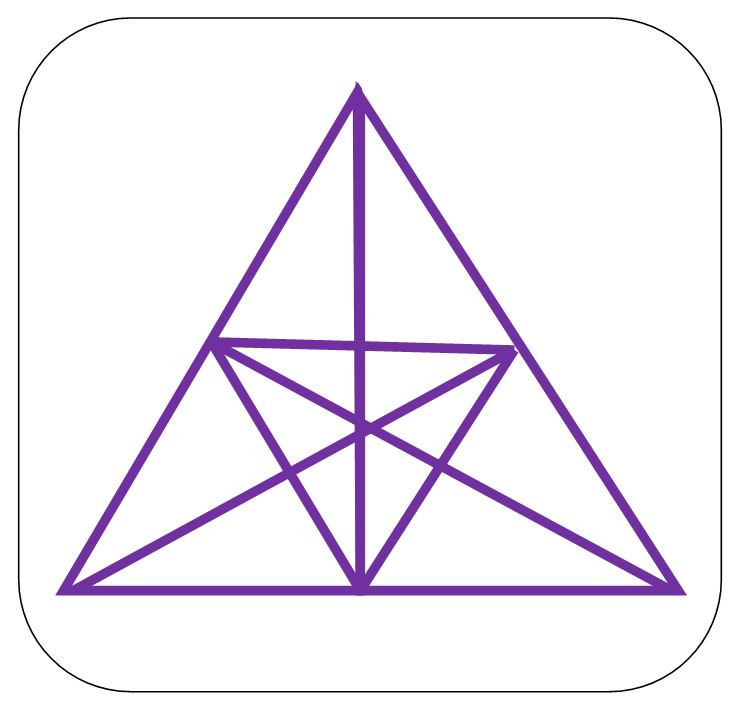
Wie viele Dreiecke erkennst du auf dem Bild unten?
Gib mir eine Antwort und ich nenne dir
deinen IQ (Intelligenzquotient)
Besser oder schlechter als 100?
Hast du 16 Dreiecke gefunden, bist du ganz schön clever. Das enspricht einem IQ von 100 = Durchschnitt! Es sind aber mehr als 16 Dreiecke. Bei gefundenen 17-20 Dreiecken liegt der IQ bei etwa 110. Willst Du besser sein? Dann bitte, zeige es mir!
Hier geht es zur Lösung der Aufgabe 3
Aufgabe 4
Welcher Stern (und warum ?) gehört nicht in die Reihe ?
Zum Vergrößern auf einen Stern klicken.
Jeder 4. Leser ist nicht in der Lage, diese Aufgabe innerhalb von 40 Sekunden zu lösen.
Vorsicht, diese Aufgabe ist schwerer als man denkt. Man erkennt 5 nebeneinander liegende Sterne. Die Aufgabe ist es, den Stern zu benennen, der nicht zu den anderen passt. Eine ähnliche Aufgabe haben Harvardstudenten in 40 Sekunden gelöst. Immerhin: 40 Sekunden wurden benötigt !! Mit einer Stop-Uhr kann jeder Leser seine eigene Lösungszeit ermitteln.
Hier kommt man zur Lösung der Aufgabe 4
Aufgabe 5
Wie viele Dreiecke erkennst du auf diesem Bild?
Hier kommt man zur Lösung der Aufgabe 5
Aufgabe 6
Zwei Freunde wollen sich 8 Liter Bier teilen; sie haben aber außer dem Gefäß, in dem sich die 8 Liter Bier befinden, nur noch zwei andere Gefäße von je 5 und 3 Litern. Wie ist das Bier zu teilen? Am Anfang haben wir also folgende Konstellation: 8 – 0 – 0
Das große 8 Liter fassende Glas ist voll, die anderen Gläser – 5 und 3 Liter fassend – sind leer.
Hier kommen Sie zur Lösungen der Aufgabe 6
Aufgabe 7
Welche Farbe hat mein Zylinder ?
Bobby und seine beiden Freunde stehen hintereinander und sehen alle in die gleiche Richtung, das heißt, der hinterste kann die Hinterköpfe der beiden vorderen sehen, und jene
r in der Mitte sieht lediglich den Hinterkopf des vordersten. Bobby steht ganz vorn und kann niemanden sehen. Umdrehen ist nicht erlaubt. Ein Zylinderverkäufer kommt dazu und setzt von seinen 5 Zylindern, die er bei sich hat – 3 weiße und 2 schwarze – jedem dieser drei Männer einen Zylinder auf den Kopf. Woher weiß Bobby, welche Farbe sein Zylinder hat ?
Nach einem Moment der Stille sagt Bobby ganz vorne stehend:
Die Farbe meines Zylinders ist …. !!
Welche Gedanken gingen Bobby durch den Kopf ?
Hier ist die Lösung zu Aufgabe 7
Aufgabe 8
Sie denken beim Anblick dieser Aufage sicher: Oh wie leicht!
Lassen sie sich aber nicht täuschen. Nur wer gut bis sehr gut in Mathematik ist, rechnet die folgenden 4 Aufgaben richtig.
Hier geht es zur Lösung der Aufgabe 8
Hier kommen die Lösungen
Hier ist die Lösung zu Aufgabe 1
Haben sie die Fehler nun entdeckt? Jetzt habe ich sie aber richtig reingelegt!
Ich verrate es ihnen: das Wort „die“ vor dem Wort „Fehler“ kommt zweimal vor.
Hier ist die Lösung zu Aufgabe 2
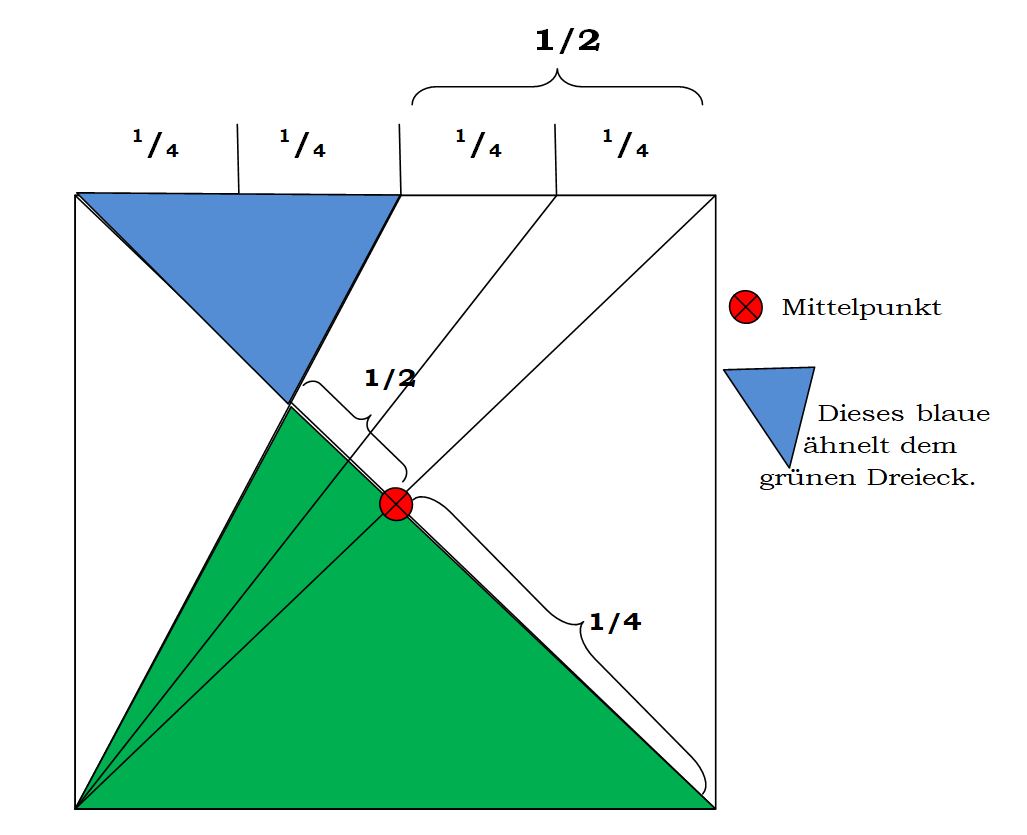
In dem Bild oben habe ich einige Zusatzlinien eingezeichnet, um es ihnen leichter zu machen. Wie ich eingangs sagte, ist die Grundseite des grünen Dreiecks 10 cm lang und die des kleinen ähnlichen Dreiecks nur halb so groß, also nur 5 cm. Wir wissen auch, dass die Höhe des grünen Dreiecks doppelt so groß sein muss wie die Höhe des kleinen – hier im Bild blau dargestellt – sogenannten ähnlichen Dreiecks. Ist nun die Höhe des großen Dreiecks doppelt so groß wie die des kleinen Dreiecks, dann verbleibt ja für die Höhe des kleinen Dreiecks nur die Hälfte des großen Dreiecks.
Das heißt wiederum: die Höhe vom großen Dreieck plus die Höhe vom kleinen Dreieck ergibt die Gesamthöhe von (in unserem Beispiel) 10 cm. Somit verbleiben für die Höhe des grünen Dreiecks 2/3 von 10 cm und 1/3 von 10 cm für das kleine hier blau gezeichnete Dreieck.
2/3 von 10 (großes grünes Dreieck) ist 6,66666 –> da Periode „6“, sagen wir der einfachheithalber 6,6
1/3 von 10 (kleines sog. ähnliches blaues Dreieck ) ist 3,33333 –> da Periode „3“ sagen wir wie oben der einfachheithalber 3,3.
Nun können wir rechnen: Das grüne große Dreick hat eine Fläche von halber Grundlinie (10:2=5) mal 6,6.
Das ist die Lösung: 5 mal 6,6666666 Periode 6 ergibt: 33,33333 Periode 3.
Die Frage war: Wie groß ist der Anteil des grünen Dreiecks bezogen auf das Quadrat?
Der Anteil beträgt genau 1/3 des Quadrates.
Hier ist die Lösung zu Aufgabe 3
Dreiecksfrage:
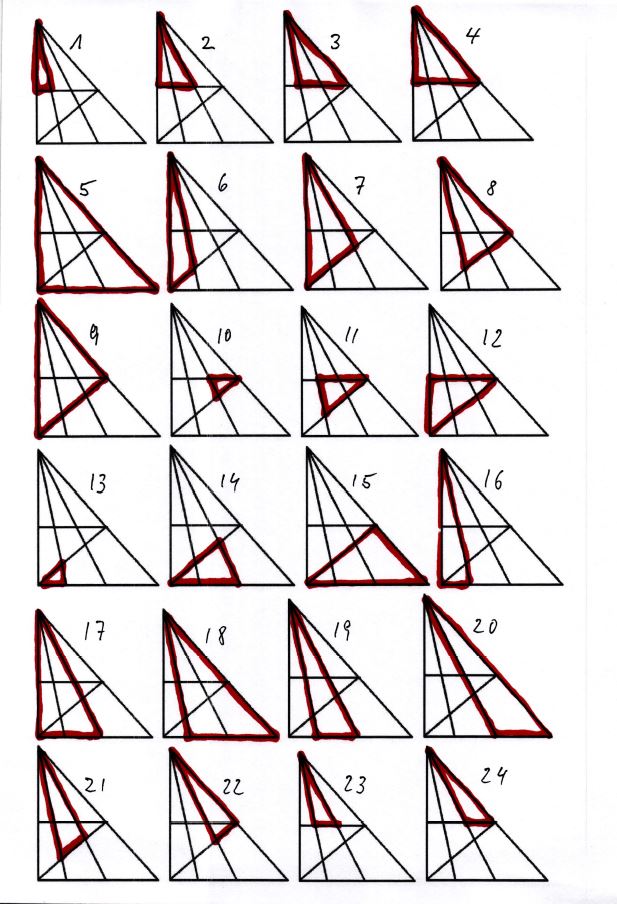
Ergebnis der Dreiecksfrage von Kapitel „Dreiecksfrage“ lautet:
24 Dreiecke!
Gewusst ohne zu mogeln? Dann beträgt dein IQ etwa 125 – 130. „LOL“
Zum Vergrößern bitte Dreiecksbild anklicken!
Hier ist die Lösung zu Aufgabe 4
Es ist der erste Stern, diese Figur –> 
Warum?
- Der zweite Stern? Eine solch leichte Aufgabe käme für einen IQ-Test nicht infrage!
- Der dritte 5-zackige Stern? Auch dies wäre keine geeignete Frage , da zu leicht!
- Der hellrote Stern? Da nur ein solcher Stern vorhanden –> zu leichter Test!
- Das kleine Stern? Wäre ja möglich, aber immer noch zu leicht!
- Was bleibt übrig? Erstaunt? Der erste Stern passt nicht in die Reihe!
Auflösung:
Alle Sterne haben eine Besonderheit, nur nicht der erste Stern!
- Der zweite Stern hat als einziger Stern keine Umrandung
- Der dritte Stern hat als einziger Stern nur 5 Zacken
- Der vierte Stern ist als einziger Stern hellrot
- Der 5. Stern ist als einziger Stern kleiner als die anderen.
- Zum ersten Stern: Dieser Stern hat als einziger Stern keine Besonderheit !!
Oder anders formuliert:
Der Stern ganz links tanzt aus der Reihe, denn er ist der einzige, der nicht einzigartig ist. Er ist sozusagen speziell, weil er nicht speziell ist.
Hast du das Rätsel wirklich innerhalb von 40 Sekunden lösen können?
Hier ist die Lösung zu Aufgabe 5
Wieviele Dreiecke findet man in diesem Bild?
Es sind genau 47 Dreiecke !!
Hier ist die Lösung zu Aufgabe 6
Zuerst gieße ich das das 5-Liter-Gefäß voll, so bleibt: 3 – 5 – 0.
Aus dem Fünfergefäß fülle ich jetzt das Dreiergefäß voll: 3 – 2 – 3
Nun gieße ich den Inhalt dieses letzten Gefäßes in das erste Gefäß: 6 – 2 – 0
Jetzt fülle ich das Bier aus dem Fünfergefäß in das Dreiergefäß, so dass das Fünfergefäß leer wird: 6 – 0 – 2
Darauf gieße ich aus dem Achtergefäß in das Fünfergefäß, alles was hineingeht, 1 – 5 – 2
Nun muss ich noch aus dem Fünfergefäß den einen Liter hinausgießen, um das Dreiergefäß ganz zu füllen, dann habe ich: 1 – 4 – 3
Die Aufgabe ist gelöst. Das eine Gefäß enthält in der Tat, die gewünschte Hälfte der acht Liter und der andere Freund kann den Inhalt der beiden anderen Gefäße zusammen nehmen.
Hier ist die Lösung zu Aufgabe 7
Es gibt fünf Zylinder, zwei schwarze und drei weiße.
Würde der hinterste also vor sich zwei schwarze Zylinder sehen, wäre das Rätsel schnell gelöst, da für ihn nur drei weiße Zylinder übrig blieben. Da er aber nichts sagt, ist davon auszugehen, dass dies nicht der Fall ist. Die ersten beiden Zylinder sind folglich nicht beide schwarz. Es bleiben die Optionen: beide weiß oder die Kombination schwarz-weiß. Der Freund in der Mitte muss davon ausgehen, dass der hinterste mitgedacht hat.
Würde der in der Mitte jetzt vor sich einen schwarzen Zylinder sehen, wüsste er, dass er selbst einen weißen Zylinder hat, denn sonst hätte der hinterste ja etwas gesagt. Sieht er vor sich einen weißen Zylinder, kann er seine eigene Farbe nicht eindeutig bestimmen. Diese Tatsache bringt wiederum dich ins Spiel. Du hast scharf nachgedacht und vertraust deinen Freunden.
Beide haben 30 Minuten lang geschwiegen, daher musst du davon ausgehen, dass sie die Farbe ihrer Zylinder nicht eindeutig bestimmen können.
Deine Antwort lautet also weiß, weil in allen anderen Fällen einer deiner Freunde eine Antwort gegeben hätte.
Hier ist die Lösung zu Aufgabe 8
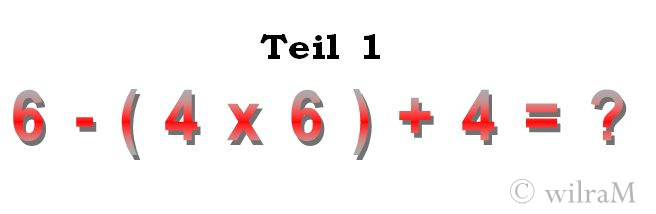Es gilt in der Mathematik: Punkt- vor Strichrechnung. Wir rechnen also: 6 – 24 + 4. Bleiben nur noch Strichrechnungen übrig, also hier das Minus- und das Plus-Zeichen, dann wird von links nach rechts, also der Reihe nach gerechnet. 6 – 24 ergibt -18. Jetzt wird 4 addiert, ergibt nach Adam Riese das Ergebnis -14
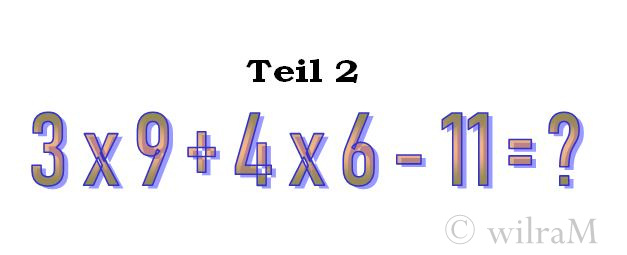Auch wieder die bekannte Regel: Punkt- vor Strichrechnung. Wir rechnen 3×9=27, 4×6=24. Es bleibt stehen: 27 + 24 – 11. Nun wieder, da nur Strichrechnung übrig geblieben ist: Erst „+“ , dann „-“ ergibt als Ergebnis 40
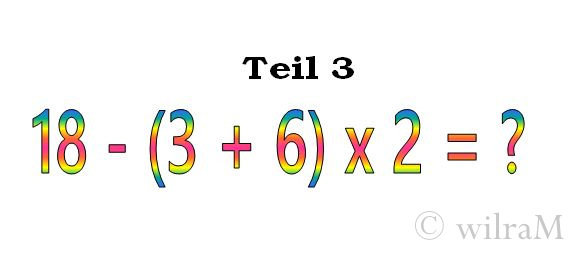Bei dieser Aufgabe gibt es zwei Lösungswege. Weg 1: Wir wissen, dass immer zuerst Klammern, wenn vorhanden, gerechnet werden. Die Klammer ist 3+6 = 9. Danach wieder Punkt- vor Strichrechnung, also Klammer 9 mal “ ergibt 18. Nun 18 minus die mit 2 multiplizierte Klammer ergibt als Ergebnis 0.
Weg 2: Das Distributiv- oder Verteilungsgesetzt besagt: Die Klammer wird ausmultipliziert. Wir rechnen also: 3 mal 2 und 6 mal 2 und erhalten 6 + 12 = 18. Nun geht es wie wie oben in Weg 1 weiter mit 18 – 18 ergibt als Ergebnis 0.
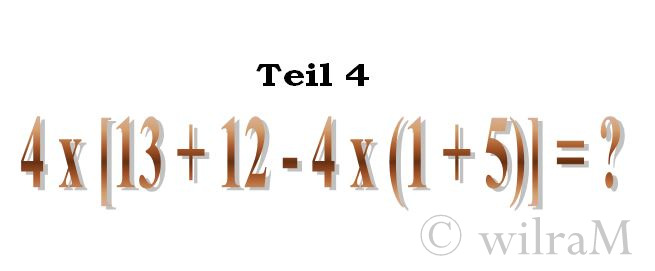Auch hier gilt wie immer: Klammer- vor Punkt-, und Punkt- vor Strichrechnung. Die Summe in der runden Klammer beträgt 1+5=6. Mit 4 multipliziert ergibt 24. Nun wird in der eckigen Klammer weitergerechnet. 13+12-24=1. Dieses Ergebnis der eckigen Klammer wird mit 4 multipliziert: 4×1=4. Wir erhalten als Ergebnis 4.
Kommentar hinterlassen